25年J题超声波定位软件部分

我的DESMOS模拟程序

官网J题

题目大致要求是：

在一个扇形范围内有一个信标，信标只有一个功能就是向扇形圆心发射超声波信号
扇形圆心直径80cm的圆内，放接收装置，接收装置捕获到超声波信号
根据捕获到的超声波信号来推算信标的位置，定位到划分出的格子内就行
无法知道信标发射超声波信号的起点时间，无法直接定位信标位置

根据讨论与思索，决定使用多探头计算时间差的方法来倒推出信标位置；另一种方法是直接用舵机旋转机构来设计，这里只分析第一种方式。

软件模拟

绘制网格图

使用desmos来绘制出题目所需扇形网格图如下

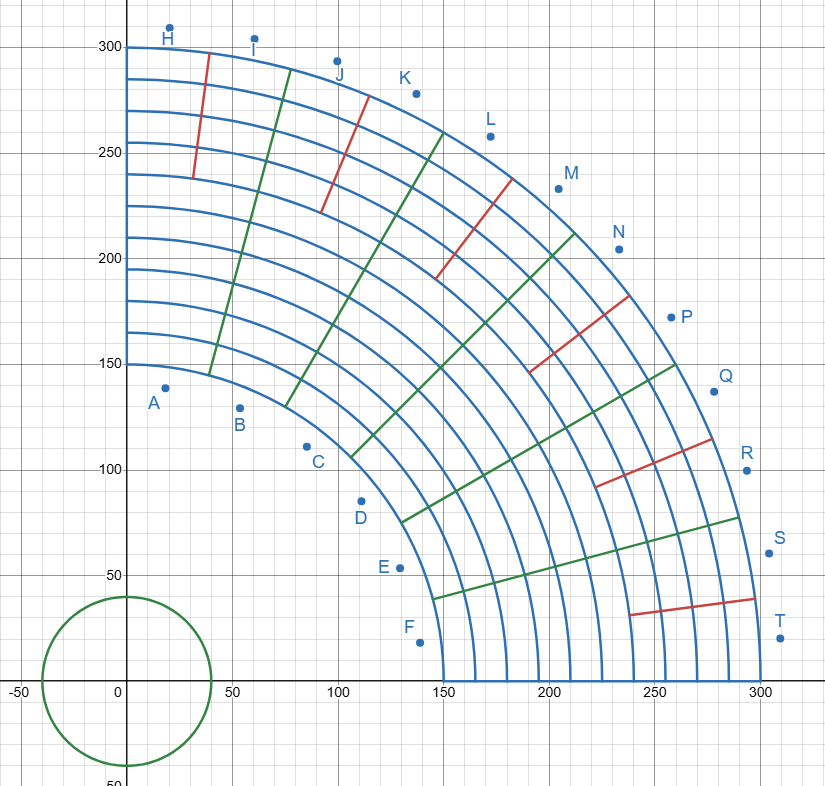
绘制信标与探头

探头位置可以随意，此处使用等边三角形分布，增加信标到接收器的距离差值，增加计算容错

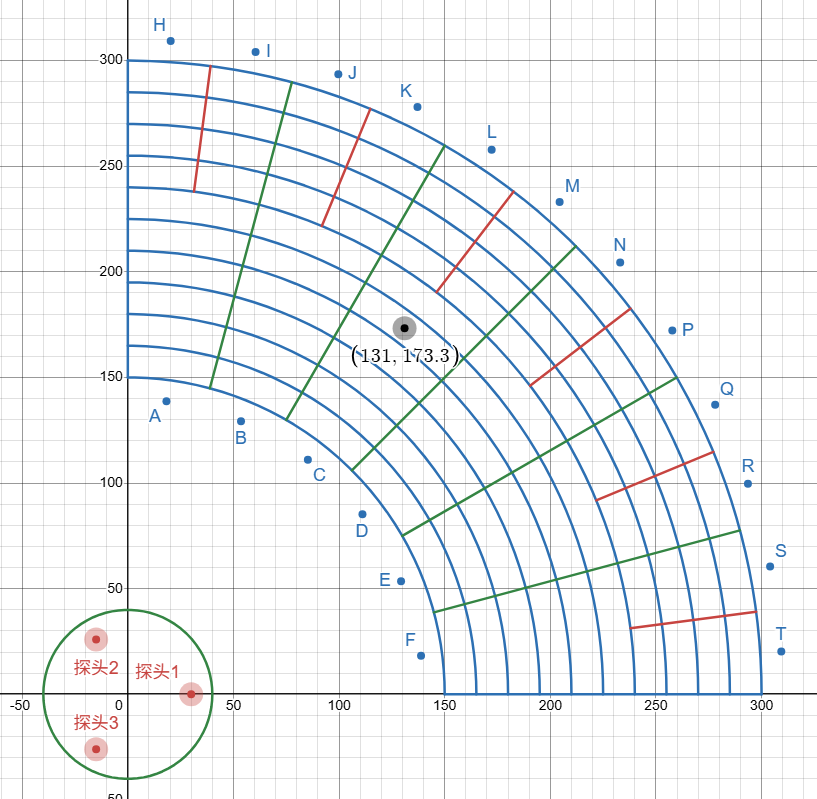
TDOA算法

在超声信标定位系统中，即使不知道超声波的初始发射时间节点，也能通过多个接收探头的信号到达时间差来实现定位，这就是所谓TDOA算法，这一过程完全符合题目对系统的要求，具体如下：

根据题目，定位装置允许拥有多个仅有接收功能的超声波探头。设信标发射超声波的时刻为t₀（未知），3 个探头接收到信号的时刻分别为t_A、t_B、t_C（可测量），则超声波从信标传播到各探头的时间为t_A−t₀、t_B−t₀、t_C−t₀。

信标到各探头的距离可表示为：

到探头 A：\(d_A=v\cdot(t_A-t_0)\)
到探头 B：\(d_B=v\cdot(t_B-t_0)\)
到探头 C：\(d_C=v\cdot(t_C-t_0)\)

其中v为超声波传播速度。当计算距离差时，t₀会被消去，例如d_A−d_B=v⋅(t_A−t_B)，仅与可测量的接收时间差相关。

结合探头的已知坐标（设为(x_A,y_A)、(x_B,y_B)、(x_C,y_C)）和信标的未知坐标(x,y)，根据距离公式可列出：

\(\sqrt{(x−x_A)^2+(y−y_A)^2}=d_A\)
\(\sqrt{(x−x_B)^2+(y−y_B)^2}=d_B\)
\(\sqrt{(x−x_C)^2+(y−y_C)^2}=d_C\)

将上述方程两两相减，可消去二次项，得到关于x和y的线性方程组，可以列出：

\(\sqrt{(x−x_A)^2+(y−y_A)^2}-\sqrt{(x−x_B)^2+(y−y_B)^2}=d_A-d_B\)
\(\sqrt{(x−x_A)^2+(y−y_A)^2}-\sqrt{(x−x_C)^2+(y−y_C)^2}=d_A-d_C\)
\(\sqrt{(x−x_B)^2+(y−y_B)^2}-\sqrt{(x−x_C)^2+(y−y_C)^2}=d_B-d_C\)

联立求解即可得到信标坐标，进而确定其所在区段。

计算差值

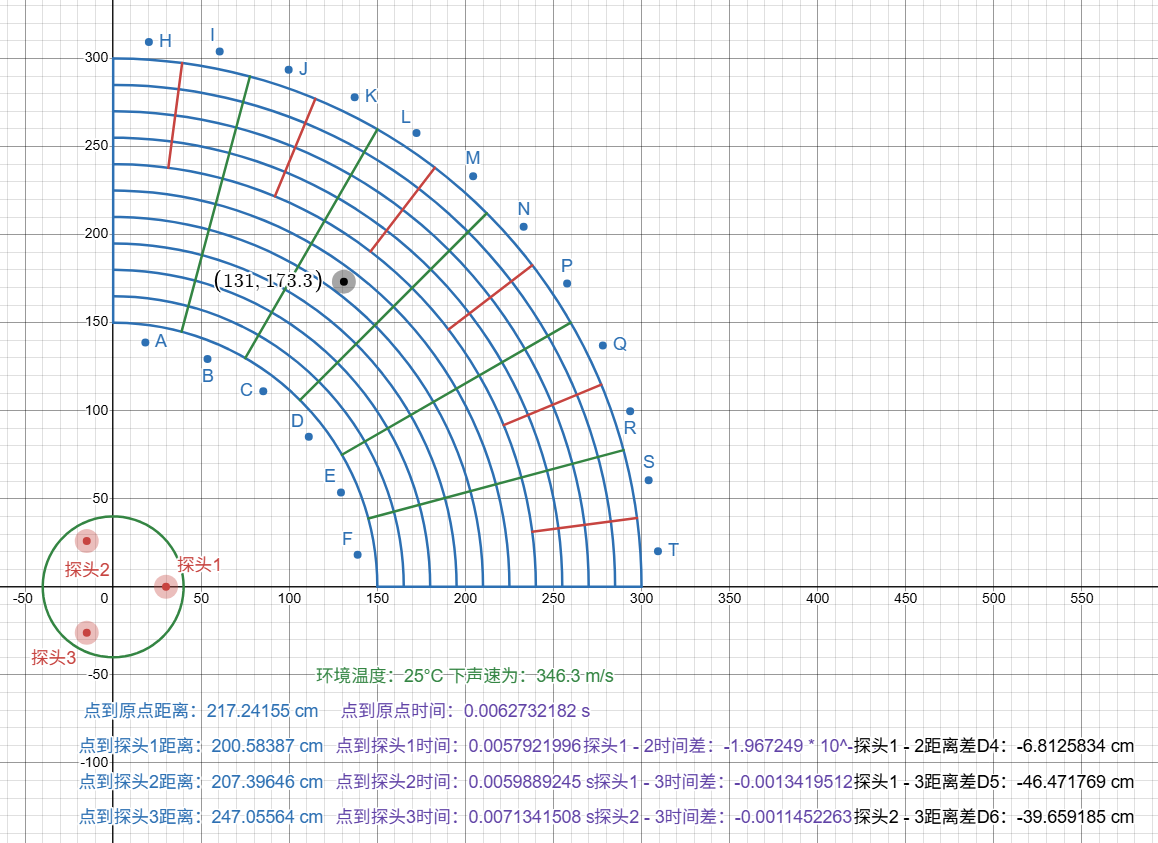
绘制关于x、y和距离差的方程组

可以看到两个方程的交点即为信标位置，由此测试出无需初始时间即可计算信标位置。

可以增加剩余一个时间差值的计算，联立计算三个方程式，计算三条线的交点来提高精度。

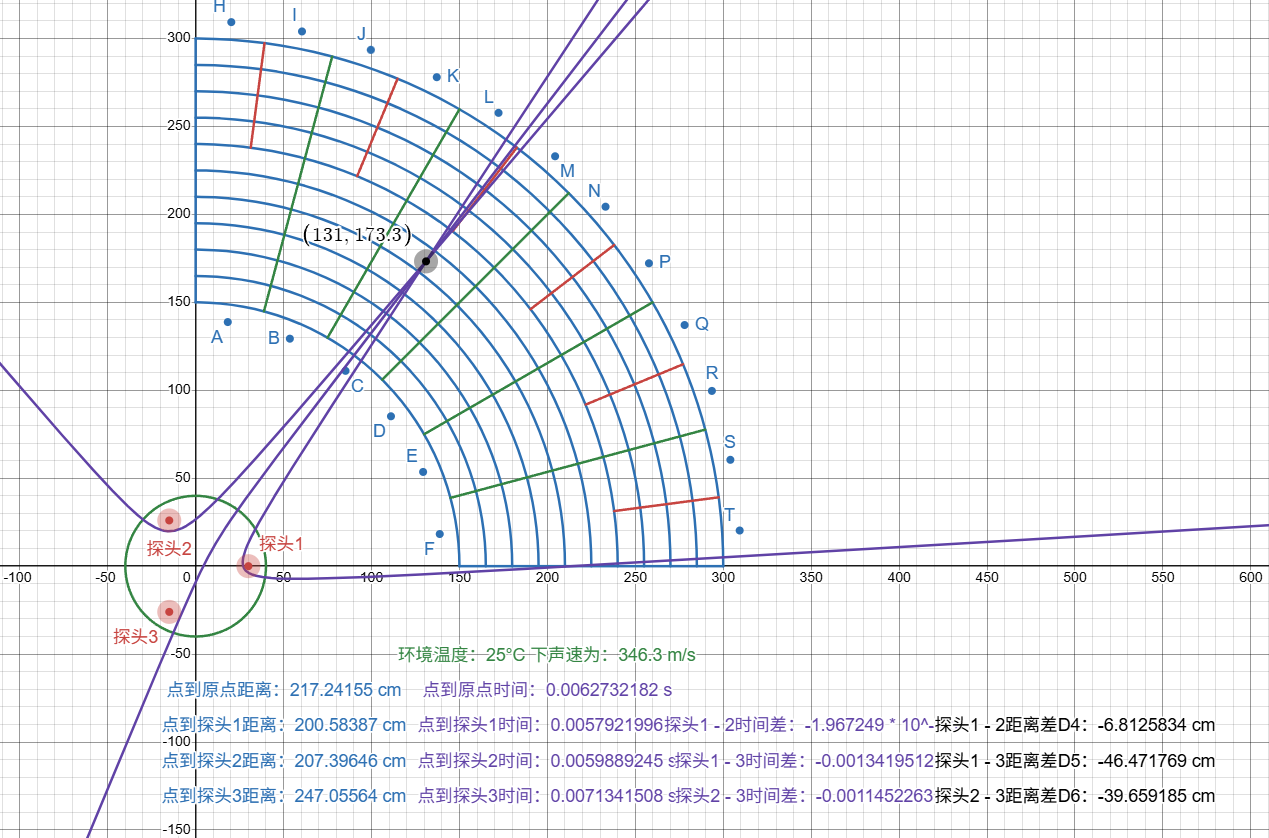
详细运算方程可以参考我的DESMOS程序网址，为了简化计算，有些运算会跳过一些没必要的运算过程，比如计算距离差就用了先前通过坐标算出的距离作差，实际应用应该是时间差*目前声速来计算。

单片机模拟计算

由于暂时实物场景还未搭建，先手动填入相应时间差与声速来计算信标坐标。

注意，这里程序依然使用两线交点计算，考虑到奇异点情况，两线选用t1-t2与t2-t3的距离差方程。

运算方式

有了上面DESMOS模拟运算的成功结果，我们接下来就只需要在单片机平台上计算那两个方程联立后的结果就行，此处我ESP32平台比较常用，因此直接在ESP32上进行模拟计算。

为了解出两个方程的值，此处使用牛顿 - 拉夫逊方法来进行计算，这种方法很适合微控制器实现，因为它只需要基本的数学运算。

牛顿 - 拉夫逊方法需要设定初始猜测值，在猜测值的基础上进行迭代，猜测值离真实值越接近，计算结果越准确。

因为单片机性能冗余，将信标可能范围进行更细的划分，每5度角度和每5单位进行划分，在150到300范围内划分出540个点，直接对每个点都进行一次计算，随后使用残差分析找到最接近的值即可。

几何退化

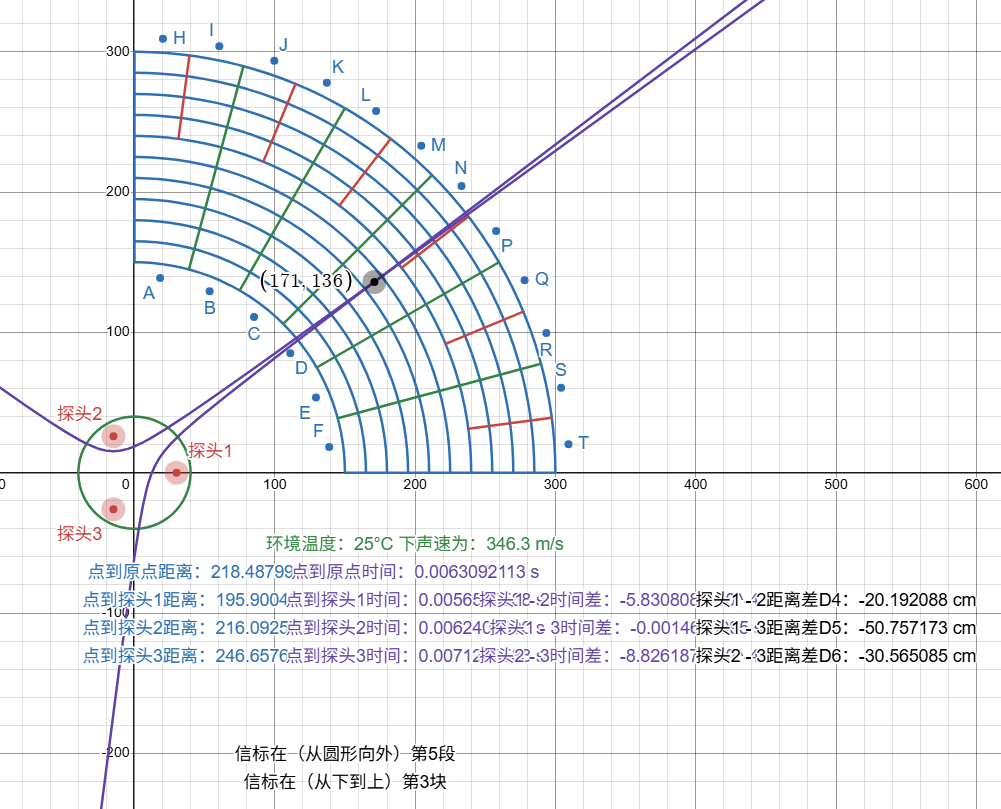
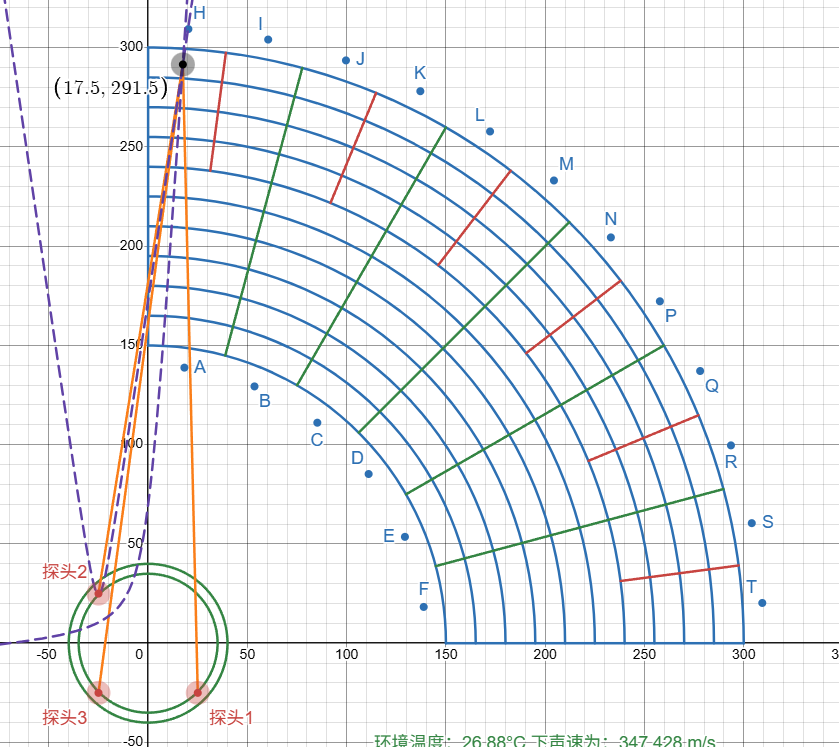
在TDOA算法中，会出现 "几何退化" 现象 —— 当信标与两个探头共线时，距离差方程会出现奇异性（雅可比矩阵行列式为 0），导致牛顿迭代无法收敛。例如下图中的情况，就是探头1与3和信标连成直线，导致t1-t3的距离差方程成为0，使得无法计算出正确坐标：

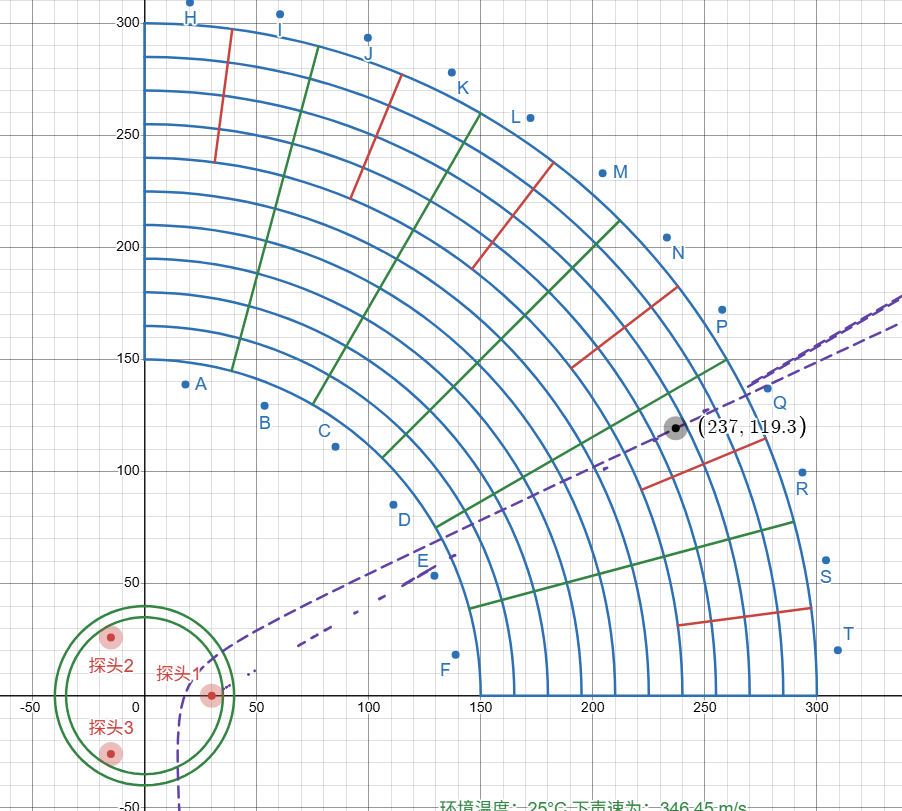
此处解决方法也简单，因为信标范围只在第一象限，因此只要将t1-t3的距离差方程换成t2-t3的即可，如下图所示，两条非线性方程经过DESMOS的模拟，无法在第一象限产生奇异点：

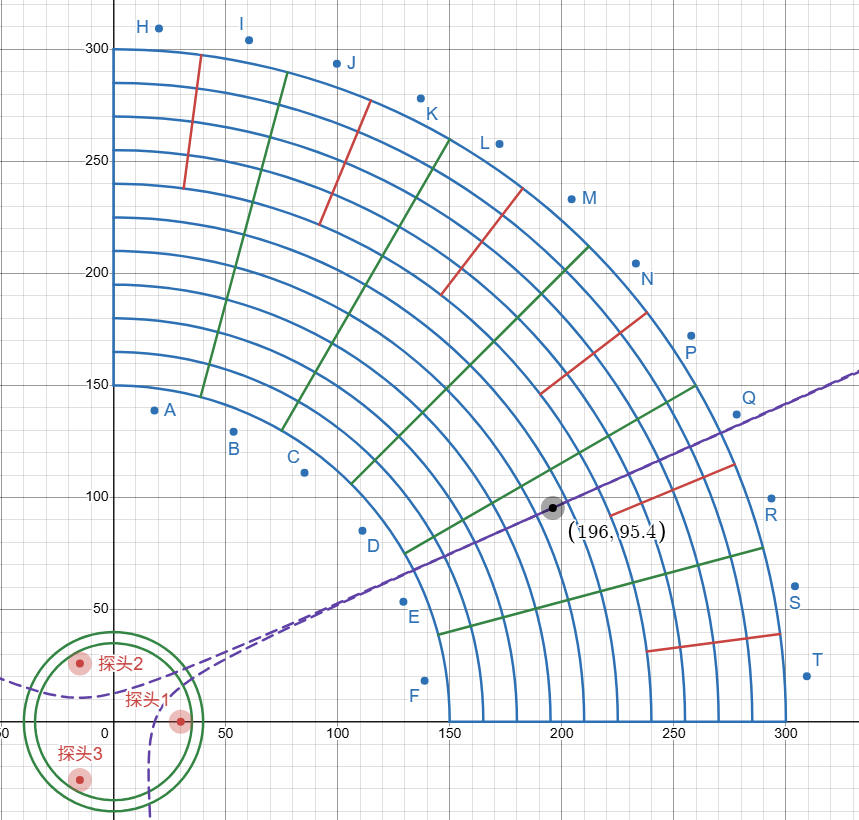
双交点问题

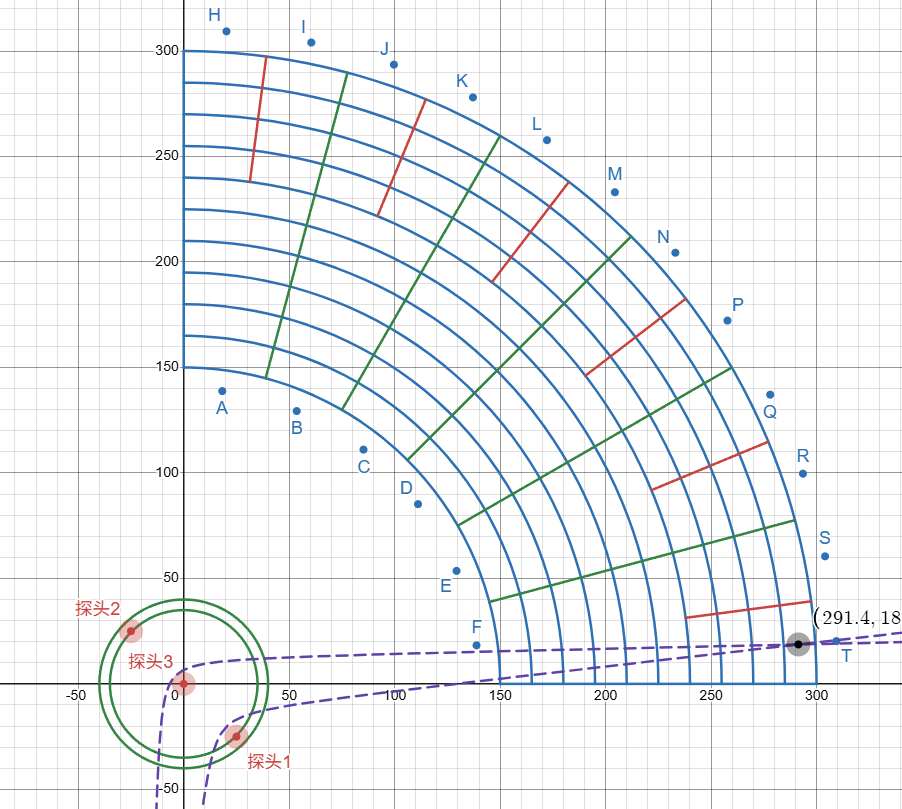
若使用t1-t2和t2-t3两个方程则还是会在过奇异点的位置也就是0到30度位置会产生两个交点，暂时无法修正牛顿迭代使之能够算出远端的交点而非近端，就会导致无法计算信标正确位置。

~~因此还是决定选用t1-t3和t2-t3两个方程，在DESMOS中模拟，第一象限内就不会出现奇异点和双交点的情况。~~

选择更改探头坐标，构成斜线面向第一象限的等腰直角三角形，来避免问题。

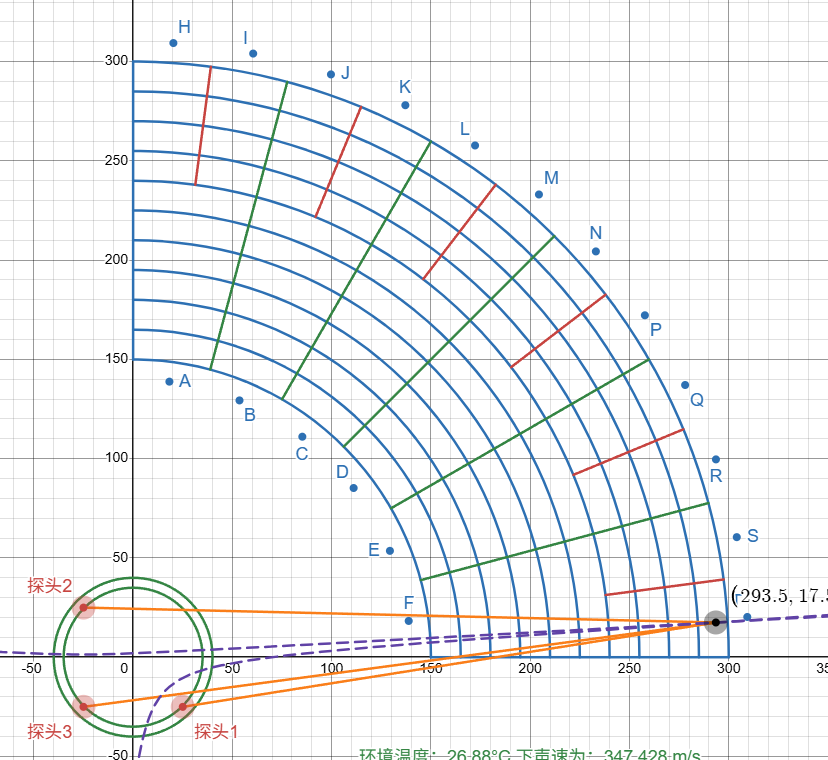
过拟合问题

上方图可以看到，信标在角度临界点附件，两条曲线图像会有拟合的趋向，导致在附近计算牛顿迭代会导致计算结果不够精确，因此改为直线分布的三点，增加临界点两条曲线的间隔大小，使得计算结果更加精确。

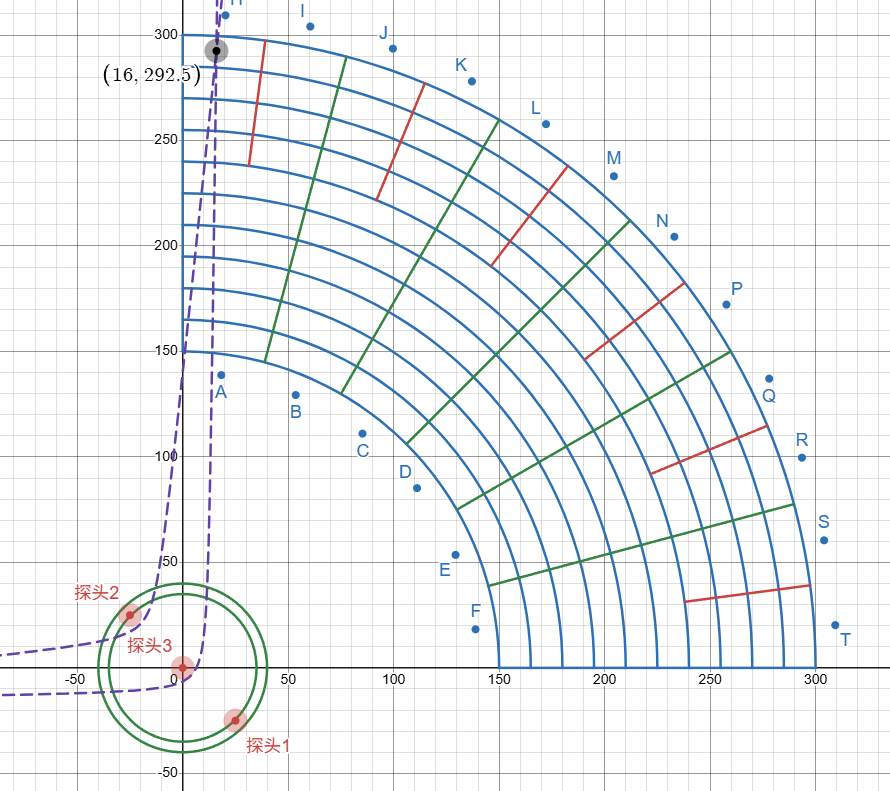
温度误差

在单片机运行测试中，发现温度也就是声速对于结果的影响较大，一位小数位（10^-1次方）的变化可能导致最后计算出格子位置偏差到相邻一格，此处就暂时先增加一个高精度的温度传感器来测量实时温度，随后根据温度计算公式\(c = 331.3 + 0.606\cdot T\) 来计算出较为准确的声速，以此提高计算精度。

后续可以增加一个外部可调参数来对温度变量进行补偿，以此减小误差。